motivation
First off, why bother pigify-ing the creation of a k-d tree? Pig is pretty much limited to problems where high latency isn't a concern and so unless the set of things we're planning on indexing is huge it doesn't make much sense to talk about it other than as a theoretical exercise. Well. Let's see...
- Suppose you wanted to create your own index of star brightness observations (of which this meager database has over 20 million). Given a set of galactic coordinates and time, what observations lie nearby in space and time? Maybe a k-d tree would help!
- Pssh, star brightness observations, that's basically only 4 dimensions, what about indexing document vectors for all the web pages in the Common Crawl data set? You could try a k-d tree.
- What about satellite data? There's an interesting (and old) project called the International Cloud Climatology Project (ISCCP). Want to know cloud properties for a region over time? Well, one of their data sets has broken the world into a grid of 30km x 30km 'pixels' and reports all sorts of interesting cloud properties for each those pixels for over 30 years! It's about 5GB of data per month... Yikes. I'm going to reach for a k-d tree to search through that beast.
problem outline
So now that we're sufficiently motivated (and come on, if stars, web pages, and clouds don't get you going then what the hell are you doing here?), let's work through a much smaller example that we can actually look at. I find with problems involving points it's most intuitive to use geo data as a starting point. Geo data is easy to think about and you can plot your results on a map for verification.
The example geo data we'll use is from the Geonames data base and is simply a list of all the cities in the world with population greater than 1000. We're going to use pig create a k-d tree containing these cities. Some ways of storing and querying this k-d tree will be discussed.
get data
Go ahead and download and unzip the data so you too can play along. I like wget.
$: wget http://download.geonames.org/export/dump/cities1000.zip $: uzip cities1000.zip
This will result in a tab-separated-values file called 'cities1000.txt'. In the following analysis we're only using the coordinates and the ids of a point. You could write your pig script to load all the fields and project out the ones you don't want or if you don't like writing gory pig schemas like me, you can cut them out ahead of time on the command line.
$: cut -f1,5,6 cities1000.txt > cities1000_cut.tsv
Where fields 1, 5, and 6 (in the cut command above) correspond to the geonameid, latitude, and longitude respectively.
algorithm
Before we can write a pig script to actually deal with this we'd better have our algorithm solidly in hand. Here it is to the best of my ability to write it...
- Break the space into non-overlapping partitions.
- Run a non-parallel k-d tree generation algorithm on the points that fall within each partition.
- Merge the k-d trees from (2) into the result k-d tree
Non-overlapping partitions wtf?
Basically we need to break the space our points fall inside into smaller pieces that don't overlap. This is important for merging the trees in the final step since, with non-overlapping pieces, a point can only belong to one partition and, consequently, exactly one tree. If a point was inside more than one partition then we'd have a heck of a time merging the trees from those partitions since there'd be collisions. No fun.
Now, which algorithm do we actually use to partition? It can get complicated since it really depends on the performance you're looking for and the distribution of your data. You don't want to send too many points to a single partition. On the other hand, processing empty or mostly empty partitions really sucks too. In the Shevtsov et al. paper I referenced at the beginning of this post they run an initial clustering algorithm over the points and choose how to partition the space dynamically based on that clustering. However, since this is a blog post and I am but one man, we'll use an ok way of partitioning based on the quadkey tiling scheme described here. This basically just chops the space up into an even grid.
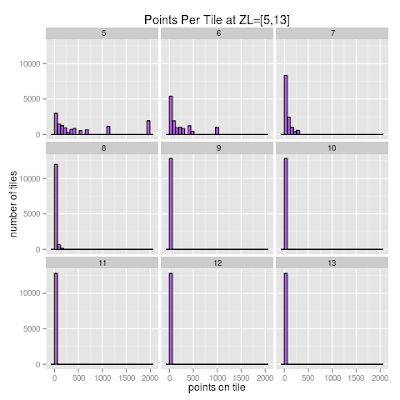
Ok, so now that I'm using tiles, how do I know what size tile to use? The quadkey system allows you to use a zoom level that ranges from 1 to 23. To pick the best one for this example I sampled the cities and generated a distribution of the number of points per tile at various resolutions:
Eyeballing it, it looks like 7 is a good zoom level at which to partition the space. Mostly it's because the distribution for 7 has an alright spread and I don't see hot spots where one partition gets waaay to many points like at levels 5 and 6. But, please, by all means, experiment with this.
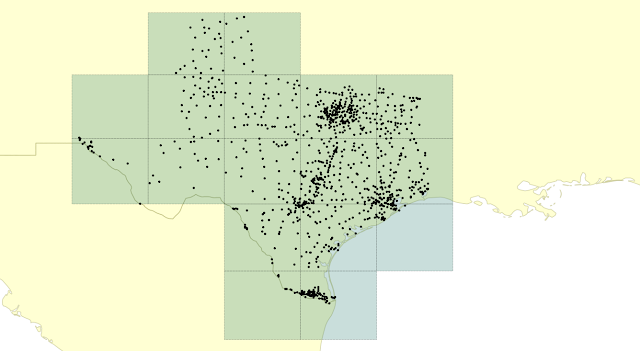
Since we're dealing with geodata and I'm in a visualization mood, here's what Texas looks like partitioned at zoom level 7. The points are the actual cities pulled from our example data set:
As you can see, what with West Texas being a wasteland and all, the partitioning makes it so that some partitions get too much data and some get very little. Marfa's got dust and Dallas has all the suburbs. You just can't win with a grid. But, we're going to march forward anyhow.
non-parallel k-d tree
Since we're going to be using pig the k-d tree generation code will need to be written as a user-defined-function (UDF). Pig is going to group the points by their quadkey which will result in a bag, one per quadkey (partition). Hence, the UDF will need to take a bag of points as input.
Here's also where it's important to think about how we're going to represent the k-d tree during the pig processing. A nested tree representation doesn't work because we need to operate on individual nodes from the pig script itself (filtering, etc). So, the UDF will yield a bag of points, exactly the same size as the input, only with the left and right children (from the k-d tree) attached as fields. Let's call the UDF "KDTree". Rather than paste a couple hundred lines of java, an implementation can be found in the sounder repo on github here. Here's the important bits:
udf signature: KDTree(points) where points is a bag with the following schema:
output schema: The output is a bag, with the same size as the input, with the following schema:
A few things. In the output, above_child and below_child correspond to the right and left children of the point. They're labeled as such since the k-d tree udf can operate on k-dimensional points, not just 2-dimensional points. is_root is an integer, 0 or 1, indicating whether the node is the root of the k-d tree or not. This is because we're returning the nodes as a completely flat structure and we need to be able to reconstruct our tree. Also, in the next step of the algorithm, we're going to need to separate the roots of each partition from the branches. axis is the axis that this node splits (either 0 or 1). This is so that, once we reconstruct our tree, we know how to search it.
udf signature: KDTree(points) where points is a bag with the following schema:
points:bag{
point:tuple(
id: chararray,
coords: tuple(
lng:double, lat:double
)
)
}
output schema: The output is a bag, with the same size as the input, with the following schema:
nodes:bag{
node:tuple(
id: chararray,
is_root: int,
axis: int,
above_child: chararray,
below_child: chararray,
coords: tuple(
lng:double, lat:double
)
)
}
A few things. In the output, above_child and below_child correspond to the right and left children of the point. They're labeled as such since the k-d tree udf can operate on k-dimensional points, not just 2-dimensional points. is_root is an integer, 0 or 1, indicating whether the node is the root of the k-d tree or not. This is because we're returning the nodes as a completely flat structure and we need to be able to reconstruct our tree. Also, in the next step of the algorithm, we're going to need to separate the roots of each partition from the branches. axis is the axis that this node splits (either 0 or 1). This is so that, once we reconstruct our tree, we know how to search it.
merging trees
This part seems complicated but it's actually pretty simple. Remember, it's only possible because we broke our original space into non-overlapping pieces. In the previous step we've generated a k-d tree for each of those pieces. As a result of this each partition has its own root node. To merge the trees we first need to nominate one of those roots (say, the median point along the longitude axis) as the top level root. Then, taking the top level root's tree to start we simply insert the other roots into this tree. Importantly, this step cannot be done (as far as I can tell) in parallel. Instead, it relies on how we ultimately choose to store (and query) the tree. I'll describe a simple way using a hashmap in a bit which can easily be extended to work with a distributed key-value store.
Implementation
Implementing this in pig is actually pretty straightforward. I'll go over each part in turn.
First, as a convenience and to make the pig code more readable, we'll use the define keyword in to alias our udfs. GetQuadKey is the udf that generates the quadkeys and KDTree is the udf to generate a k-d tree from a bag of points.
define GetQuadkey sounder.pig.geo.GetQuadkey(); define KDTree sounder.pig.points.KDTree();Next, we simply load the data using pig's default PigStorage class with tabs as the field delimiter.
data = load '$POINTS' as (id:chararray, lat:double, lng:double);Then we generate a quadkey for every point at resolution 7. We're also using pig's built in TOTUPLE operator since the k-d tree udf needs points to be specified as tuples of coordinates. This is so it can handle k-dimensional points and not just 2-dimensional points.
with_key = foreach data generate id, TOTUPLE(lng, lat) as point, GetQuadkey(lng, lat, 7) as quadkey;And here's the meat of it where we group by quadkey (effectively using hadoop to partition our space) which collects all the points for a given partition into a single bag. This is fed to the k-d tree udf which does the work of creating the k-d trees.
trees = foreach (group with_key by quadkey) {
tree = KDTree(with_key.(id, point));
generate
group as quadkey,
FLATTEN(tree) as (id:chararray, is_root:int, axis:int, above_child:chararray, below_child:chararray, point:tuple(lng:double, lat:double));
};
Finally, the trees are split into roots (remember, each partition will have its own root) and branches. These are flattened to pull the coordinates out of their tuple containers and stored separately. The roots and branches need to be dealt with differently when creating the final k-d tree so they're stored separately to reflect that.
flat_trees = foreach trees generate id..below_child, flatten(point) as (lng, lat); split flat_trees into roots if is_root==1, branches if is_root==0; store roots into '$ROOTS'; store branches into '$BRANCHES';
Running
So let's go ahead and run that on our cities data. I saved the pig code above into a file called 'generate_kdtree.pig'. To run:$: pig -p POINTS=cities1000_cut.tsv -p ROOTS=cities1000/roots -p BRANCHES=cities1000/branches generate_kdtree.pig
This should generate only one map-reduce job and result in a directory on the hdfs which contains the roots and branches of the k-d trees.
As a sanity check, here's an image of what texas looks like, now with the roots:
Since the first splitting axis in the k-d tree algorithm is the x-axis (longitude) we expect the root of each k-d tree to be the median point along that axis in its respective partition. By eyeballing every partition (I sure do a lot of eyeballing...) this appears to be true. So yay, looks good.
Also, notice I'm getting ahead of myself a bit and showing the root I've nominated as the top level node.
Final Tree
This part takes some care. First, we need to decide how we're actually going to store and query the k-d tree. Directly from the hdfs in its current form is definitely not going to work. For illustrative purposes I'm going to use a ruby hash to store and query the tree. This, of course, only works because the data is small enough to fit into memory. However, most distributed key-value stores and other, more complex nosql stores like cassandra and hbase, would work as well. For the purposes of this example you can think of them as giant ruby hashmaps too. The same basic query interface would work, just with a different data store backend.
As steps:
- Insert all the branches into the key-value store using the point id as the key and the rest of the point metadata as the value. Importantly the coordinates and the above_child and below_child are stored. How you do this is up to you.
- Nominate one of the roots as the top level root. Ideally this will be the median point along either the x or y axis. The idea here is that the number of partitions, thus the number of roots, will be small enough that finding the median point and nominating it as the root should be a simple single process problem.
- Insert the remaining roots into the key-value store using the standard k-d tree insertion procedure outlined in the wikipedia article
Of course you'll have to implement some basic k-d tree searching and insertion code, but that's a well understood problem. There are plenty of examples, eg here and here. My implementation can be found in the sounder repo on github here.
To use my code simply bring the cities1000/roots and cities1000/branches down to your local filesystem and run:
$: bin/test_built_tree.rb roots branches 0.00194469216500055 #< struct KDTree::Node id="4671654", axis=1, left="4698809", right="4723734", coords=[-97.74306, 30.26715]> $: grep -i "4671654" cities1000.txt 4671654 Austin Austin AUS,Austin,Austino,Austinopolis,Aŭstino,Gorad Oscin,Ostin,Ostina,Ostinas,ao si ting,astin,astyn, tgzas,awstn, tksas,oseutin,ostina,osutin,xxstin,Ώστιν,Горад Осцін,Остин,Остін,Օսթին,אוסטין,آستین، تگزاس,آسٹن,آسٹن، ٹیکساس,أوستن، تكساس,ऑस्टिन,ஆஸ்டின்,ഓസ്റ്റിൻ,ออสติน,ოსტინი,オースティン,奧斯汀,오스틴 30.26715 -97.74306 P PPLA US TX 453 790390 149 165 America/Chicago 2011-05-14
One test. Yes, surely that's all you need to be convinced, right?
So it works. Hurray! k-d trees with pig.